因果推断入门
这篇文章将以非常简练的方式对因果推断的基础进行总结归纳。具体教程查看最后的“参考资料”部分。
因果问题渗透到日常问题中,例如弄清楚如何提高销售额,但它们也在我们非常个人和宝贵的困境中发挥重要作用:我是否必须上一所昂贵的学校才能在生活中取得成功(是吗?教育导致收入)?移民是否会降低我找到工作的机会(移民是否会导致失业率上升)?向穷人汇款会降低犯罪率吗?不管你在哪个领域,很可能你已经或将不得不回答某种类型的因果问题。不幸的是,对于 ML,我们不能依靠相关类型预测来解决它们。
基本定义
- 是否干预(介入): $ T_i=\begin{cases}1\text{ if unit i received the treatment} \ 0\mathrm{~otherwise}&\end{cases} $
- 单元$i$的观察变量: $Y_i$
- 经过处理的结果: $Y_1$, 未经过处理的结果 $Y_0$
- 平均处理效果(average treatment effect): $ATE=E[Y_1-Y_0]$
- 被干预者的平均处理效果(average treatment effect on the treated): $ATT=E[Y_1-Y_0|T=1]$
经过干预后的效果差异,是由干预本身的效果(ATT),加上干预前的差异(偏差)一起产生的。
公式表示如下:
$$ E[Y|T=1]-E[Y|T=0]=\underbrace{E[Y_1-Y_0|T=1]}_{ATT}+\underbrace{{E[Y_0|T=1]-E[Y_0|T=0]}}_{BIAS} $$
如果偏差项 $\underbrace{{E[Y_0|T=1]-E[Y_0|T=0]}}_{BIAS}$ 消失,那么关联将会成为因果关系,手段的差异成为因果效应。
$$ E[Y|T=1]-E[Y|T=0]=E[Y_1-Y_0|T=1]=ATT=ATE $$
那么,我们可以进行随机实验消除偏差。
随机实验
如果干预组和对照组相同或具有可比性,除了他们接受的干预外,关联将是因果关系。或者,用更专业的话说,当未处理的结果等于处理的反事实结果时。
随机实验包括将群体中的个体随机分配到干预组或对照组,随机化通过使潜在结果独立于干预来消除偏见。 $$ (Y_0,Y_1)\perp T $$ 也就意味着干预是唯一在干预和对照中产生结果差异的因素。
$$ E[Y|T=1]-E[Y|T=0]=E[Y]=E[Y_1-Y_0]=ATE$$
最危险的公式
Moivre 公式: $SE=\frac\sigma{\sqrt{n}}$
其中 $SE$是平均值的标准误差,$\sigma$是标准偏差,$n$是样本大小,如果等式左右两侧进行平方,那么所表示的是方差的均值。 Moivre 方程表示了一种不确定性,这种不确定性随着我们观察到的数据量的增加而缩小。相反的,如果数据量过小,那么可能会得到极高或者极低的值。
** 置信区间(ci) ** 我们估计的标准误差(confidence intervals)是置信度的衡量标准。使用标准误差,我们可以创建一个区间,该区间将包含 95% 的时间的真实平均值。从统计理论中,我们知道 95% 的正态分布的质量介于均值上下 2 个标准差之间。
置信区间是一种为我们的估计设置不确定性的方法。样本量越小,标准误越大,置信区间越宽。
假设检验
包含不确定性的另一种方法是陈述假设检验:均值差异在统计上与零(或任何其他值)不同吗?
$$ N(\mu_1,\sigma_1^2)-N(\mu_2,\sigma_2^2)=N(\mu_1-\mu_2,\sigma_1^2+\sigma_2^2)$$ $$ N(\mu_1,\sigma_1^2)+N(\mu_2,\sigma_2^2)=N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$$
两个正态分布的均值差以及标准差的差值表示为:
$$\mu_{diff}=\mu_1-\mu_2$$ $$SE_{diff}=\sqrt{SE_1+SE_2}=\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}$$
$z$ 统计量
$z$ 统计量衡量观察到的差异的极端程度。为了检验均值差异在统计上不同于零的假设,我们将使用矛盾。我们将假设相反的情况是正确的,即我们将假设差异为零。这称为零假设,或 $H_0$ 。然后,我们会问自己“如果真正的差异确实为零,我们是否可能会观察到这种差异?”在统计数学术语中,我们可以将这个问题转化为检查 z 统计量离零有多远。
$$z=\frac{\mu_{diff}-H_0}{SE_{diff}}=\frac{(\mu_1-\mu_2)-H_0}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}$$
在 $H_0$ 下,$z$ 统计量遵循标准正态分布。因此,如果差异确实为零,我们将在 95% 的时间内看到 z 统计量在平均值的 2 个标准差内。这样做的直接后果是,如果 z 高于或低于 2 个标准差,我们可以以 95% 的置信度拒绝原假设。
p值
我们能准确估计这个机会是多少吗?我们观察到这样一个极值的可能性有多大?输入 $p$ 值!“$p$ 值是获得测试结果的概率至少与测试期间实际观察到的结果一样极端,假设原假设是正确的” .
更简洁地说,$p$ 值是看到此类数据的概率,前提是原假设为真。如果原假设为真,它衡量您看到测量结果的可能性有多大。自然地,这常常与原假设为真的概率混淆。注意这里的区别。 $p$ 值不是 $P(H_0|Data)$,而是 $P(Data|H_0)$。
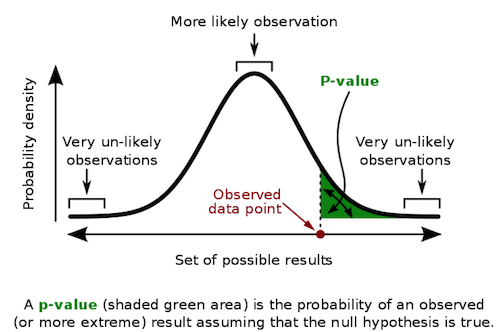
要获得 $p$ 值,我们需要计算 $z$ 统计量之前或之后的标准正态分布下的面积。 请注意 $p$ 值的有趣之处,因为它避免了我们必须指定置信水平,例如 95% 或 99%。 但是,如果我们希望报告一个,根据 $p$ 值,我们确切地知道我们的测试将通过或失败的置信度。 例如,$p$ 值为 0.0027,我们知道我们在 0.2% 的水平上具有显着性。
图因果模型
图形模型是因果关系的语言。它们不仅是您用来与其他勇敢而真实的因果关系爱好者交谈的工具,也是您用来使自己的想法更清晰的工具。
让我们以潜在结果的条件独立性为第一个例子来展开讲解。这个条件是我们在进行因果推断时需要为真的主要假设之一: $$(Y_0,Y_1)\perp T|X$$
独立性和条件独立性是因果推理的核心。因果图模型是一种表示因果关系如何起作用的方式,即是什么导致了什么。
条件独立性使我们有可能衡量完全由于干预对结果产生的影响,而不是任何其他潜伏在周围的变量。
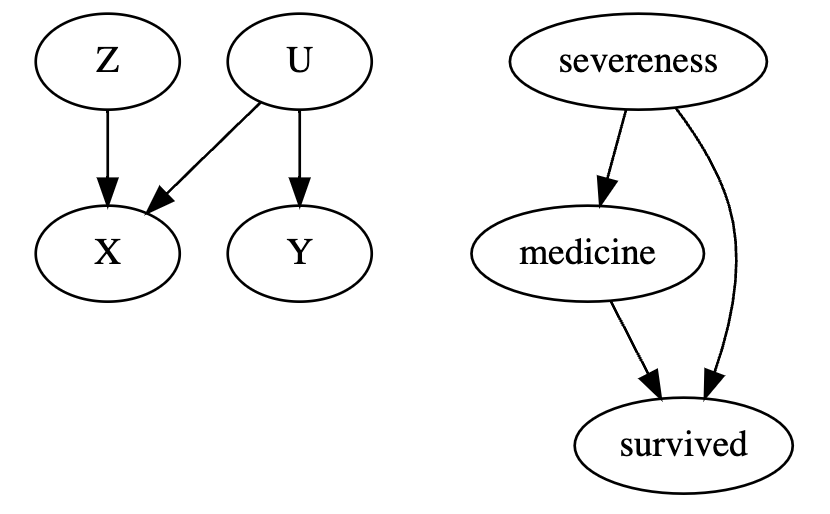
在上面的第一个图形模型中,我们说 Z 导致 X,U 导致 X 和 Y。疾病严重程度会同时导致服药的干预和病人的存活,服药本身也带来病人的存活。
1. 单向因果
作为一般规则,当我们以中间变量 B 为条件时,从 A 到 C 的直接路径中的依赖流被阻塞。
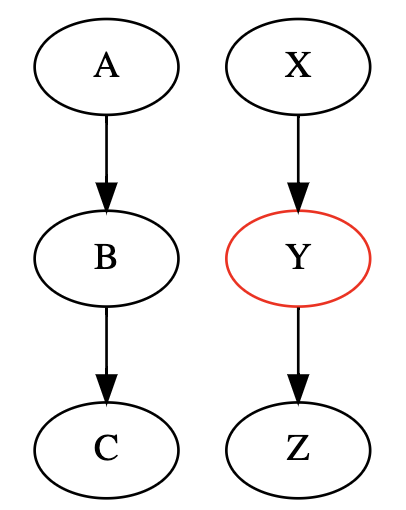
用数学表达式表达为:
$$A \not\perp C$$
或者
$$A \perp C | B$$
2. 向下分叉
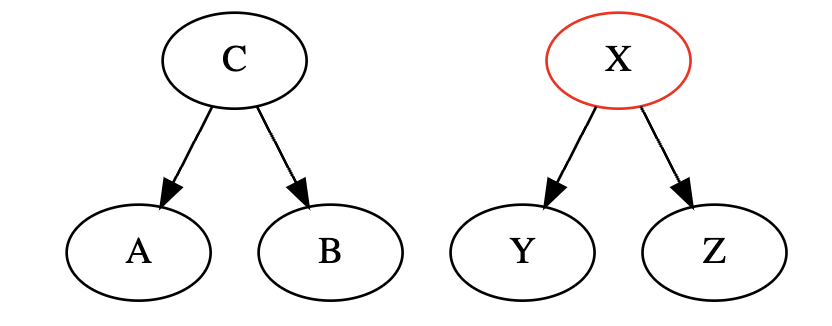
$$A \not\perp B$$
或者
$$A \perp B | C$$
3. 冲突结构
当两个箭头在单个变量上相遇,我们就称这种现象为冲突。我们可以说,在这种情况下,两个变量共享一个共同的效果。
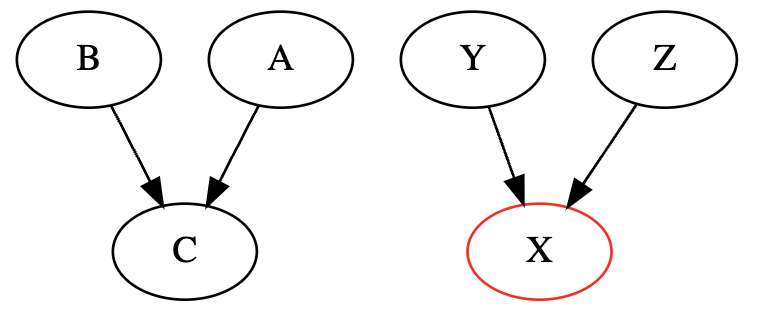
$$A \perp B$$
或者
$$A \not \perp B | C$$
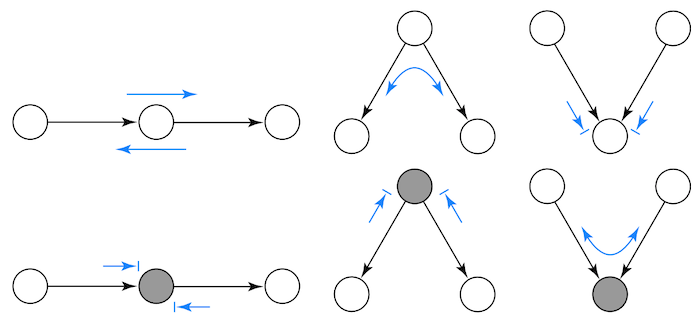
知道了这三种结构,我们可以推导出更一般的规则。一条路径被阻塞当且仅当:
它包含一个被条件化的非冲突因子 它包含一个没有被条件化的冲突因子并且没有被条件化的后代。
这里的翻译比较生硬,我把原文贴出来
Note
Knowing the three structures, we can derive an even more general rule. A path is blocked if and only if:
- It contains a non collider that has been conditioned on
- It contains a collider that has not been conditioned on and has no descendants that have been conditioned on.
所有的情况
这是一个关于依赖如何在图中流动的备忘单。尖端带线的箭头表示独立,尖端不带线的箭头表示依赖,如下图所示。
选择偏差
偏见的第二个重要来源是我们所说的选择偏见。如果当我们不控制共同原因时会发生混杂偏差,那么选择偏差与效果更相关。需要注意的是,经济学家倾向于将各种偏见称为选择偏见。通常,当我们控制的变量多于应有的变量时,就会出现选择偏差。可能的情况是,治疗和潜在结果在某种程度上是独立的,但一旦我们以对撞机为条件,就会变得依赖。
当我们以治疗的中介为条件时,类似的事情也会发生。中介变量是治疗和结果之间的变量。它确实调解了因果效应。
为了给出潜在的结果参数,我们知道,由于随机化,偏差为零 $E[Y_0|T=0] - E[Y_0|T=1] = 0$。然而,如果我们以白领个人为条件,我们有 $E[Y_0|T=0, WC=1] > E[Y_0|T=1, WC=1]$。那是因为那些即使没有受过教育也能找到一份白领工作的人可能比那些需要教育帮助才能得到同样工作的人更努力工作。同理,$E[Y_0|T=0, WC=0] > E[Y_0|T=1, WC=0]$ 因为那些即使受过教育也没有得到白领工作的人可能比那些没有工作但也没有受过任何教育的人更努力。
对中介者的调节会引起负面偏见。这使得教育的效果看起来比实际效果要低。之所以如此,是因为因果效应是积极的。如果效果是负面的,那么对中介者的调节就会产生积极的偏见。在所有情况下,这种调节都会使效果看起来比实际情况要弱。
偏差小结
第一个是混淆,当治疗和结果有一个我们无法解释或控制的共同原因时,就会发生这种情况。第二个是由于对共同效应的调节而导致的选择偏差。第三种结构也是选择偏差的一种形式,这次是由于对中介变量的过度控制造成的。即使治疗是随机分配的,这种过度的控制也可能导致偏差。选择偏差通常可以通过什么都不做来解决,这就是为什么它是危险的。由于我们偏向于行动,我们倾向于认为控制事物的想法是聪明的,因为它们弊大于利。